算法：约瑟夫环

一、前言

夫拉维·约瑟夫是公元一世纪历史学家，传说中由于他的数学天赋，得以在犹太罗马战争期间活下来。关于他的故事，有这样一个版本：

在犹太罗马战争期间，他们41名犹太反抗者困在罗马人包围的洞穴中。这些反抗者宁愿自杀也不愿被活捉，于是决定围成一个圈圈。沿着这个圈圈每两个人杀死一个，直到剩下最后两个人为止。但是约瑟夫和一个未被告发的同谋者不希望无谓地自杀，于是他迅速计算出他和朋友在圈圈中应该站的位置。

《具体数学》第二版 1.3

我们对这个问题做一层抽象和简化：假设有 n 个人围成一圈，编号是 1 到 n。从 1 开始计数，每隔一个，抹去一个，直到剩下一个人，请问这个人的编号是多少？

本文将围绕这个问题，逐层深入，探讨问题的本质。这里会涉及到链表、递归、bit数组等概念，重点在推理过程。在继续阅读之前，建议读者拿出纸和笔，思考5-10分钟，脑海中有一个初步的想法再继续读下去。

二、整理思路

首先，我们尝试理解一下该算法的过程。假设 n = 10，根据对算法描述的直接理解，会走下面这个过程：

（下划线表示在上一轮就已经被删除）

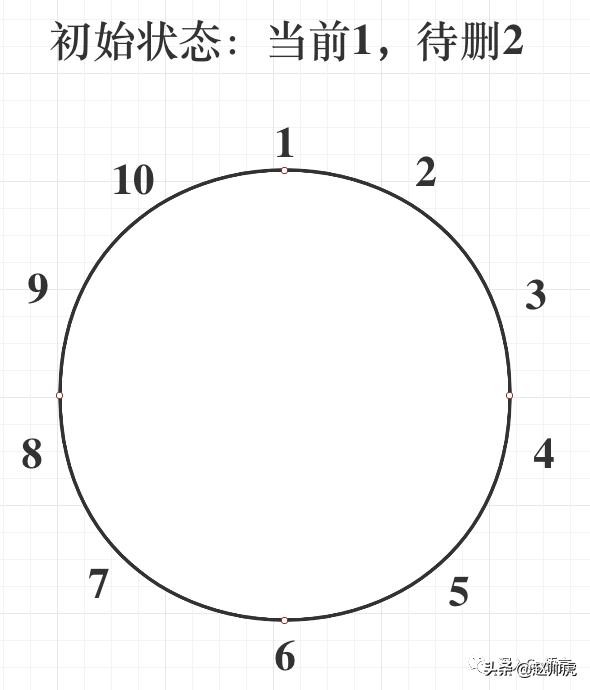
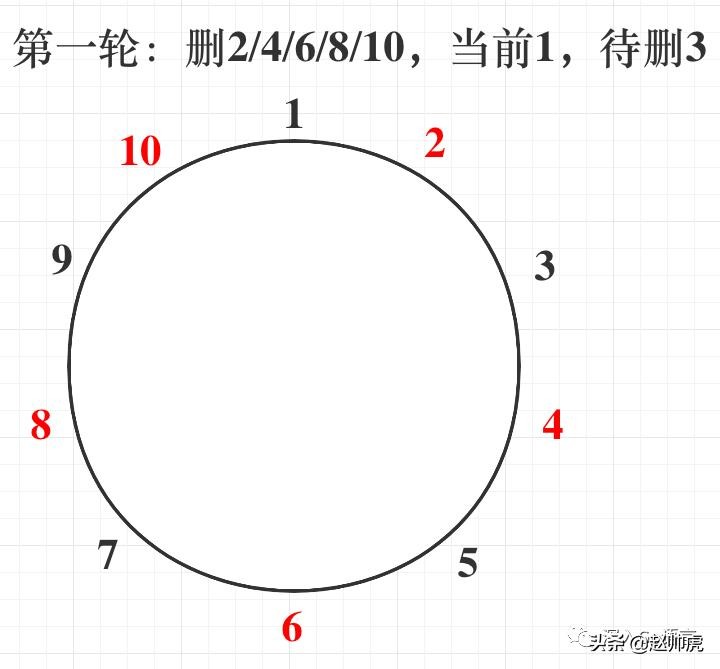
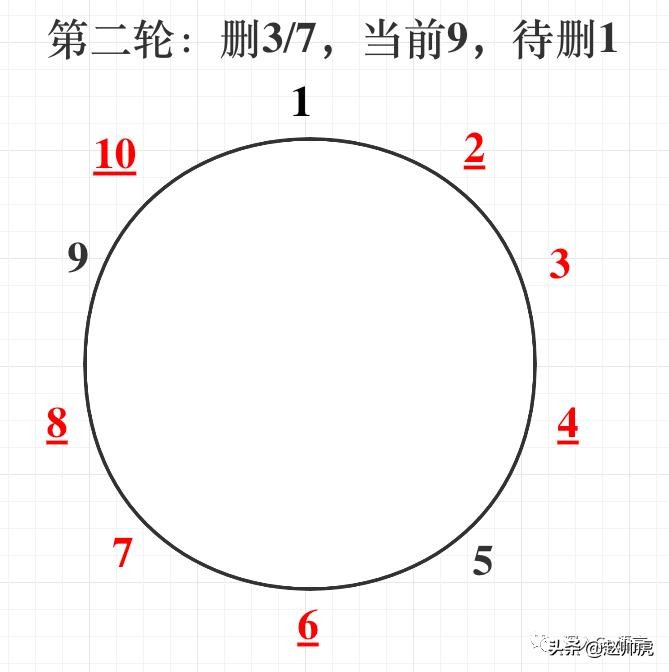
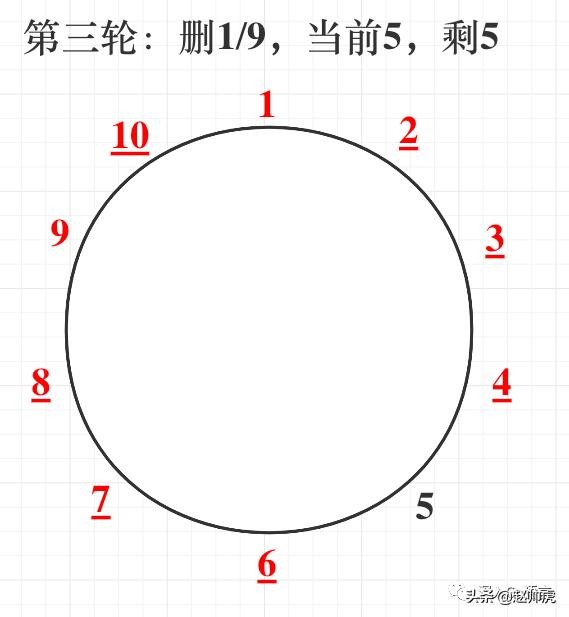
将该过程可视化呈现以后，最直观的解决方案就有了，即使用 bitmap 存储每个数字的状态(默认为0)，每次遍历更新一组数字的状态，直到仅有一个数字状态为 0。

这种方法每次都要遍历整个数组，每次遍历以后，状态为0的元素个数减半，所以需要遍历 logn 次，算法的整体时间复杂度是 O(n*logn)，空间复杂度是 O(n)。下面是基于 Go 的实现：

// JosephusBitMap 基于 bitmap 实现 // 为了简化代码，使用 []bool 替代 bitmap func JosephusBitMap(n int) int {  bitmap := make([]bool, n, n)  toDel := false  for left := n; left > 1; { for idx := 0; idx < n; idx++ {  if bitmap[idx] { continue  }  if toDel { bitmap[idx] = true toDel = false left--  } else { toDel = true  } }  }  // 读取结果  for i := 0; i < n; i++ { if !bitmap[i] {  return i + 1 }  }  return -1 }

上面这段代码中，我们使用 []bool 存储 n 个节点的状态信息，toDel 用于记录该节点是否需要被删除。由于该方法每次都需要扫描所有 n 个节点，效率并不理想。

怎么样才能不扫描所有 n 个节点呢？显然，不扫描所有 n 个节点，意味着只需要扫描未被删除的节点，有两种解决方案：

将未删除的节点拷贝出来使用环形链表

方案1的核心逻辑不是删节点，而是将未删除的节点拷贝到另一个长度 n/2 的数组。这样减少了遍历次数，但是会带来 O(logn) 次内存分配和销毁。实现高并发服务时，过多的gc并不是一件好事，所以相对于bitmap方案孰优孰劣还不好说。

方案2中的环形链表在视觉上能准确地描述约瑟夫环。实现时，需要先根据 n 初始化一个环形链表，从值1的节点开始遍历，每隔一个删除一个，直到当前节点的下一个节点是它自己。该方案也需要分配n次内存，并进行n次销毁。与方案1不同的是，初始化和销毁的只是一个节点，而不是一个数组。为了对bitmap和linkedlist 两种方案的性能有直接的对比，我们也实现一下，代码如下：

// JosephusLinklist 是基于环形链表的实现 func JosephusLinklist(n int) int {  // 初始化环形链表  head := &Node{val: 1}  cur := head  for i := 2; i <= n; i++ { cur.next = &Node{val: i} cur = cur.next  }  cur.next = head  // 删除节点  for cur := head; ; { next := cur.next cur.next = next.next cur = cur.next // 终止条件：只有一个节点 if cur.next == cur {  return cur.val }  }  // 返回结果  return -1 }

Benchmark 结果还是有些出乎预料。n=10 时，bitmap 方案的性能是 LinkedList 方案的5倍；n=10000时，bitmap 方案的性能是 LinkedList 方案的3倍。Benchmark 结果说明了很多事情，大家自行脑补。

2020-04$ go test --bench=. --benchmem goos: darwin goarch: amd64 pkg: github.com/oscarzhao/oscarzhao.github.io/assets/2020-04 BenchmarkJosephusBitMap10-4 19414291  58.8 ns/op  16 B/op  1 allocs/op BenchmarkJosephusBitMap10000-4 12986 94531 ns/op10240 B/op  1 allocs/op BenchmarkJosephusLinklist10-43978577295 ns/op 160 B/op 10 allocs/op BenchmarkJosephusLinklist10000-43256319925 ns/op  160000 B/op  10000 allocs/op PASS ok  github.com/oscarzhao/oscarzhao.github.io/assets/2020-04 5.854s

事情到这里还没有结束，我们仍然在寻找更高效的解决方案。

不忘初心，方得始终。

我们回归到问题本身，不知道还有多少人记得这张图：

朋友，你是否已发现，经过第一轮过滤以后，剩下 1/3/5/7/9，当前节点还是1。对比 n=5 的情形，会发现 n=10 问题的解是：

// f 是求解函数 f(10) = 2*f(5)-1

朋友，你是否很开心，但又有很多问号？

问号1: 这条规则是否对于所有偶数都适用？问号2: 奇数的话，怎么处理？

针对问号1，答案是 yes！具体原因不做介绍。针对问号2，我们不妨以 n=11 为例，第一轮执行结束后，结果如下：

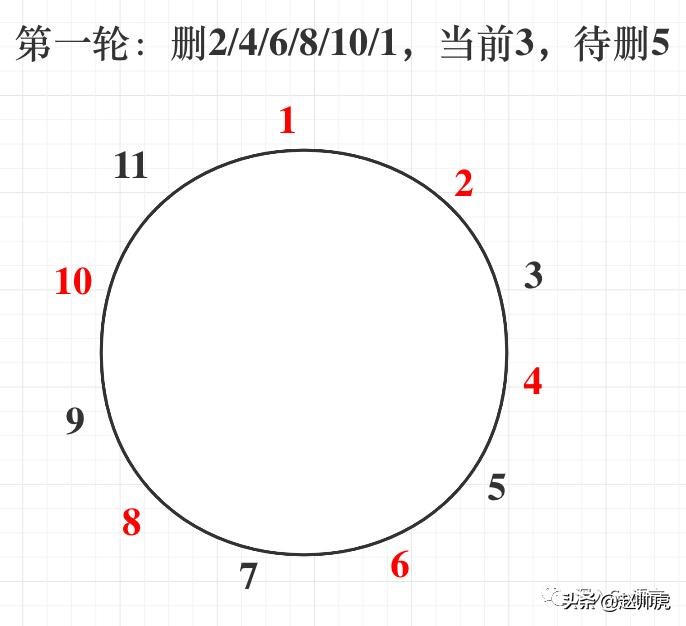
剩下的数字是 3、5、7、9、11，当前位置是3。对比 n=5 的情形，会发现 n=11 的解是：

// f 是求解函数 f(11) = 2*f(5)+1

同样，对于所有奇数，该递归式也是成立的。整合一下递归式，可以得到：

f(1) = 1 f(2*n)= 2*f(n) - 1 f(2*n+1) = 2*f(n) + 1

该方法的时间复杂度是 O(logn), 空间复杂度为1，且没有额外的内存分配。转换成代码如下：

func JosephusRecursion(n int) int {  if n == 1 { return 1  }  if n%2 == 1 { return 2*JosephusRecursion(n/2) - 1  } else { return 2*JosephusRecursion(n/2) + 1  } }

Benchmark 的结果也非常漂亮，在 n=10000 时，执行效率远超前两种实现：

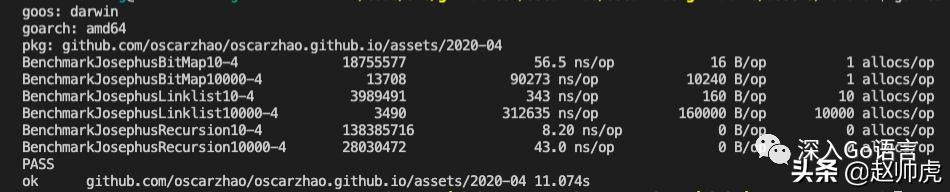
对于一个常规的计算机程序来说，时间复杂度 O(logn) 已经非常不错了。但是我们可以把问题再向前推进一步：是否存在一个 O(1) 的解法？如果这种方法真的存在，那么必须不是递归，而是通过 n 直接映射到最终结果。

考虑到是映射，我们可以借助前面的实现，打印一张映射表，给我们提供一些思路。我们使用 JosephusRecursion 打印出 n=1-20对应的结果：

shuaihu@local:2020-04$ go test --run=TestJosephusTable 1,  1 2,  1 3,  3 4,  1 5,  3 6,  5 7,  7 8,  1 9,  3 10,  5 11,  7 12,  9 13, 11 14, 13 15, 15 16,  1 17,  3 18,  5 19,  7 20,  9 PASS ok  github.com/oscarzhao/oscarzhao.github.io/assets/2020-04 0.010s

我们稍微观察一下，做一下处理，显示成这样：

1 |  1 -------- 2 |  1 3 |  3 -------- 4 |  1 5 |  3 6 |  5 7 |  7 -------- 8 |  1 9 |  3 10 |  5 11 |  7 12 |  9 13 | 11 14 | 13 15 | 15 -------- 16 |  1 17 |  3 18 |  5 19 |  7 20 |  9

然后可以得到下面一组结论：

f(2^k) = 1f(2^k + 1) = 3f(2^k + 2) = 5f(2^(k+1) -1) = 2^(k+1) - 1

结论4 等价于

f(2^k + (2^k-1)) = 2^k + (2^k -1)

处理成通用的公式就是：

f(2^k + i) = 2*i + 1, for i in [0, 2^k-1]

此时，n = 2^k + i。那么问题来了，这个公式可以推广到所有整数 n 吗？我们用数学归纳法尝试推导一下。

数学归纳法的证明分为两步：

证明当n=0时命题成立。证明如果在n=k时命题成立，那么可以推导出在n=k+1时命题也成立。（m代表任意自然数）

在我们这个case里，我们已经有四个命题：

// 基础命题 f(1) = 1 // 对所有正整数 n 都成立的命题 f(2*n)= 2*f(n) - 1 f(2*n+1) = 2*f(n) + 1 // n <= 20 才成立的命题 f(2^k + i) = 2*i + 1, 当 n = 2^k + i

我们要验证：是否对于所有 n = 2^k+i, f(2^k + i) = 2*i+1 都成立。为了能使用前面三个命题进行推导，我们把 i 分为奇数和偶数两类，分别证明：

假设n是偶数，即 n =2^(k+1)+2m,当i=2m，  => f(n) = f(2^(k+1) + 2m)  => f(n) = f(2( 2^k + m))  => f(n) = 2f(2^k + m) - 1  => f(n) = 2(2m+1) - 1  => f(n) = 2(i+1) - 1  => f(n) = 2*i + 1

同样的方法，可以证明 i 是奇数时，推导也成立。

综上所述，对于所有 n = 2^k + i, f(n) = 2*i + 1。

截止目前，我们已经拿到了 n -> f(n) 的映射关系，如何转换成代码呢？我们知道 i 和 n 的关系，但需要一个可编程的方法根据 n 求出 i。回头看看映射表，显然二进制是一个方向。这里通过一个 测试用例将结果打印出来：

func TestJosephusTable(t *testing.T) {  fmt.Printf(" n,f(n), i| %5s, %5s, %5s\n", "n_bit", "fn_bi", "i_bit")  for i := 1; i <= 20; i++ { res := JosephusRecursion(i) fmt.Printf("%2d, %2d, %2d| %05b, %05b, %05b\n", i, res, res/2, i, res, res/2)  } }

执行结果是：

2020-04$ go test --run=TestJosephusTable n,f(n), i| n_bit, fn_bi, i_bit 1,  1,  0| 00001, 00001, 00000 2,  1,  0| 00010, 00001, 00000 3,  3,  1| 00011, 00011, 00001 4,  1,  0| 00100, 00001, 00000 5,  3,  1| 00101, 00011, 00001 6,  5,  2| 00110, 00101, 00010 7,  7,  3| 00111, 00111, 00011 8,  1,  0| 01000, 00001, 00000 9,  3,  1| 01001, 00011, 00001 10,  5,  2| 01010, 00101, 00010 11,  7,  3| 01011, 00111, 00011 12,  9,  4| 01100, 01001, 00100 13, 11,  5| 01101, 01011, 00101 14, 13,  6| 01110, 01101, 00110 15, 15,  7| 01111, 01111, 00111 16,  1,  0| 10000, 00001, 00000 17,  3,  1| 10001, 00011, 00001 18,  5,  2| 10010, 00101, 00010 19,  7,  3| 10011, 00111, 00011 20,  9,  4| 10100, 01001, 00100 PASS ok  github.com/oscarzhao/oscarzhao.github.io/assets/2020-04 0.010s

对比 n_bit, fn_bi, i_bit 后，我们很难发现 n_bit 和 fn_bit 的关系，但是 n_bit 和 i_bit 的关系比较明显：把 n_bit 最高位的 1 去掉，就是 i_bit。由于 f(n) = 2 * i + 1，所以

fn_bi = (i_bit << 1) + 1

事实上，不打印二进制结果，只观察 n 和 i 的关系也能看出点端倪。这个切入点更符合我的思考过程，然后才去考虑代码实现，引入二进制表示。

截止目前，在二进制上我们已经有了可行的解决方案，这里我们借助于 golang bits 库进行操作：

func JosephusBit(n int) int {  uintN := uint(n)  leftMove := bits.UintSize - bits.LeadingZeros(uintN) - 1  mask := (uint(1) << leftMove) - 1  i := mask & uintN  return int(i*2 + 1) }

计算机硬件层面原生支持二进制运算，理论上性能会不错。我们跑一组benchmark看看：

goos: darwin goarch: amd64 pkg: github.com/oscarzhao/oscarzhao.github.io/assets/2020-04 BenchmarkJosephusBitMap10-41787387460.3 ns/op BenchmarkJosephusBitMap10000-41400175533 ns/op BenchmarkJosephusLinklist10-4  4624140 253 ns/op BenchmarkJosephusLinklist10000-4  3920  273205 ns/op BenchmarkJosephusRecursion10-41663381406.90 ns/op BenchmarkJosephusRecursion10000-4 3506577033.8 ns/op BenchmarkJosephusBit10-410000000001.02 ns/op BenchmarkJosephusBit10000-4 10000000001.01 ns/op PASS ok  github.com/oscarzhao/oscarzhao.github.io/assets/2020-04 11.982s

1.02 ns/op，性能不会随着 n 变大而衰减，且没有额外的内存分配，堪称完美。

三、延伸一下

上面的问题是约瑟夫环的一个特例，我们稍微修改一下问题：从每两个人杀掉一个，改成每 k 个人杀掉一个。这个问题还有通用的解法吗？

不妨将这个问题抽象成一个函数 f(n, d int), d 的默认值是 2。问题的答案是，存在通用的解法。由于文章篇幅限制，这里只给一个简单的指引。上面提到了我们的递归式：

f(1) = 1 f(2*n)= 2*f(n) - 1 f(2*n+1) = 2*f(n) + 1

这是 d = 2 时的特例，将这个递归式推广以后，可以得到另一个式子：

f(1) = a; f(2*n+j)=2*f(n)+b_j，当j=0,1，n>=1时

这里 a = 1, b_0 = -1, b_1 = 1。将 n 转化为二进制形式，对这个公式进行推导，并延伸得到另一组公式：

f(j) = a_j，当 1 <= j < d 时 f(d*n+j)=c*f(n)+b_j，当0<=j